Physical Modelling
AI can do many things that humans cannot. For example, it can process huge amounts of data. AI can also extract the smallest nuances in data. Finally, it is an objective description of e.g. sensations, which are otherwise very subjective in verbal description.
Nevertheless, AI has limitations. One limitation is that AI simulates a brain. Like us, AI only knows what it has been taught. Thus, it always has a limited view. Also, so-called echo chambers arise. If an AI detects a pattern, then this is recognized as typical and suggested to a user again and again. This corresponds to a prejudice, so it is very human, but often not intentional.
An alternative to AI that avoids such problems is Physical Modeling. There, the individual physically existing parts of a system with their interactions are set up as a model of reality. This can be musicians in an ensemble interacting with their musical instruments, with the room in which they play music, and with their fellow musicians.


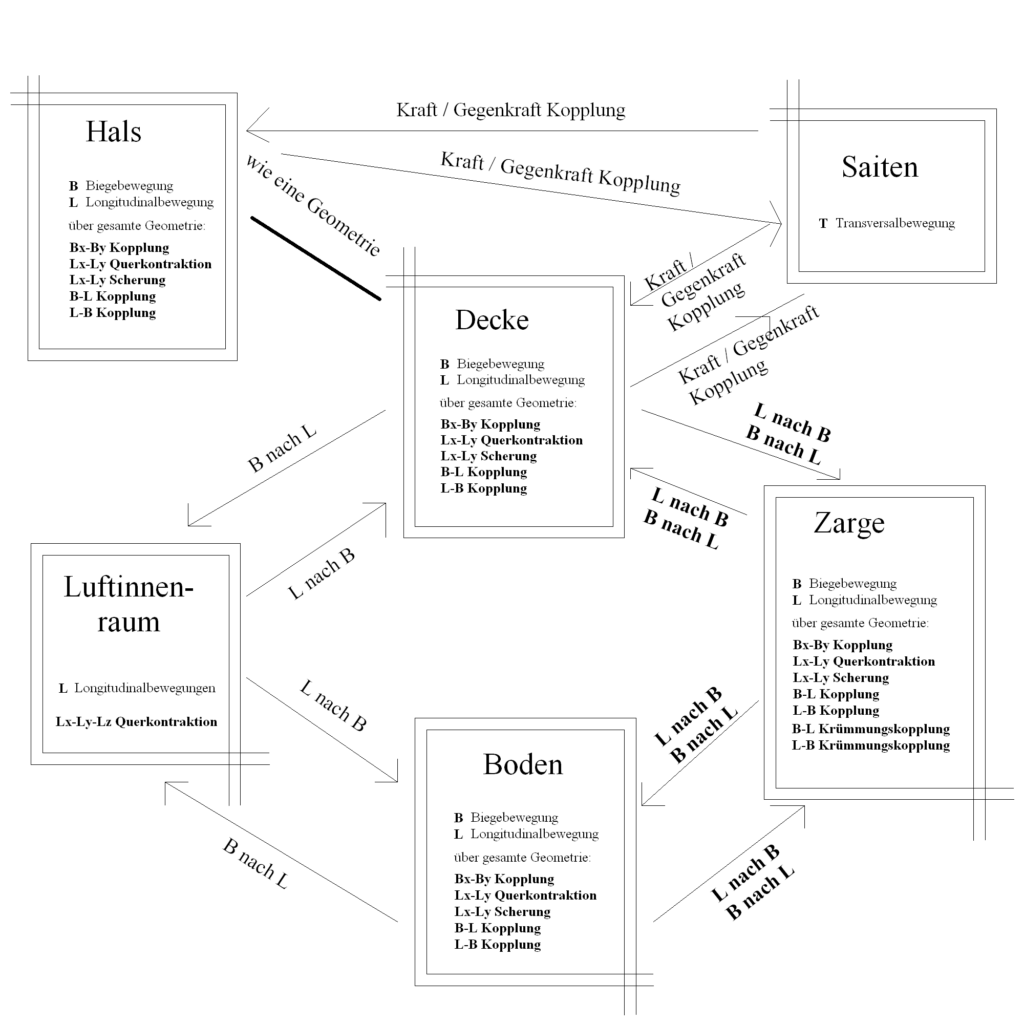
But these can also be individual parts of a musical instrument, so in the case of a guitar, for example, string, top, bottom tlate, air cavity, etc. This can be a brain, in which individual neurons interact with each other, resulting in the overall brain activity. This can also be a whole society, i.e. including economy, politics or international relations. Since Physical Modeling models real physics, it can also include ecology, animals, plants, water or climate.
This is also how the brain works, in which nerve impulses are exchanged between nerve cells, whereby a nerve cell only sends out a new impulse when it has been stimulated by other nerve cells, i.e. these have sent their impulses to the nerve cell. The brain is thus constantly synchronizing and de-synchronizing. In music, this corresponds to musical tension and relaxation. Electronic dance music (EDM), techno or dubstep often build up long arcs of tension, which then suddenly break off as the bass drum kicks in in a four-to-the-floor groove. In classical music, the cadence of chords I-IV-V-I has a tension progression. There are also longer tension progressions there like in EDM. Our brain synchronizes more and more, towards an expected tension peak, only to de-synchronize again.
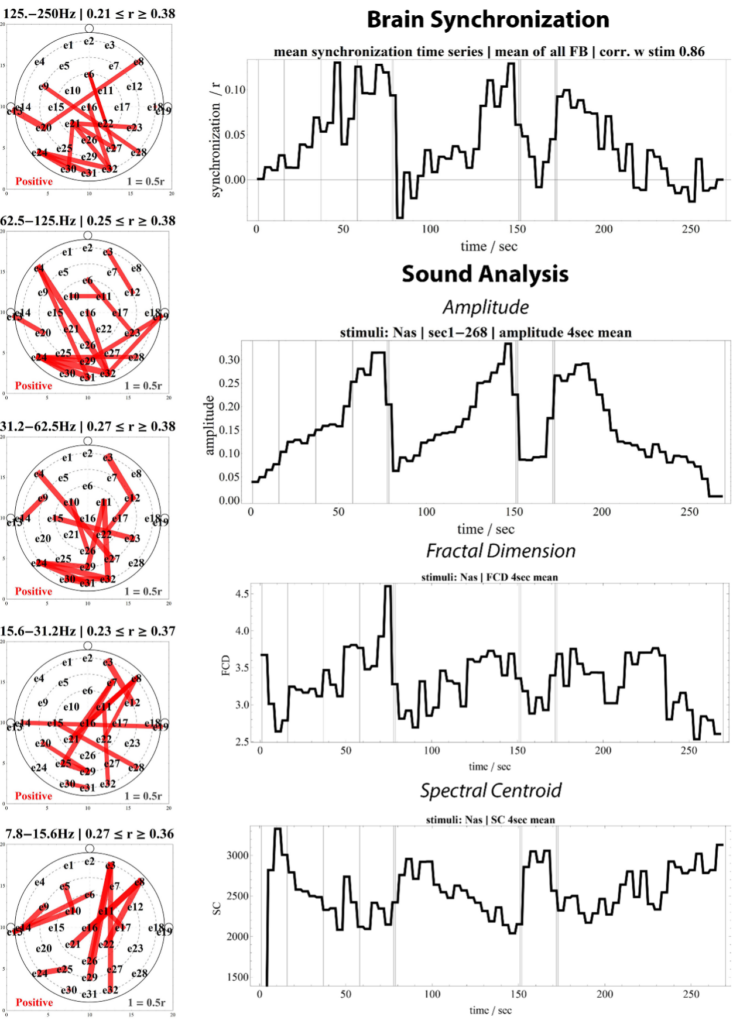
At the top right of the image we see the synchronization of the brain measured by EEG in a person listening to an EDM piece. The curve corresponds to the voltage curve of the piece, which can be seen in the analyses of the piece as shown below. Here, the Amplitude corresponds to the Loudness, the Fractal Dimension corresponds to the Complexity, and the Spectral Centroid corresponds to the Brightness of the piece. On the left side we see the networks in the brain that synchronize during the piece. These are very complex and change frequently.
The Physical Culture Theory, which uses Physical Modeling as a method, models these interactions mathematically using an Impulse Pattern Formulation (IPF). This assumes energy pulses that travel back and forth between the actors of a system. Starting from a point of view within the system, an impulse is emitted, arrives at other actors, is complexly processed or attenuated by them, returns to the starting point and causes it again to emit a new impulse.
This can be observed with a violin string. When the bow is torn from the string, an impulse is created which spreads along the string, is reflected at the ends and returns to the bow. There it tears-off the bow again and thus an impulse pattern is created, the violin tone.
This results in the most complicated patterns in the system, they are called bifurcations, bi-stable states or chaos. But a system can also ‘agree’ on a stable state. The result is often a chaotic and hardly overseeable sequence of impulses.
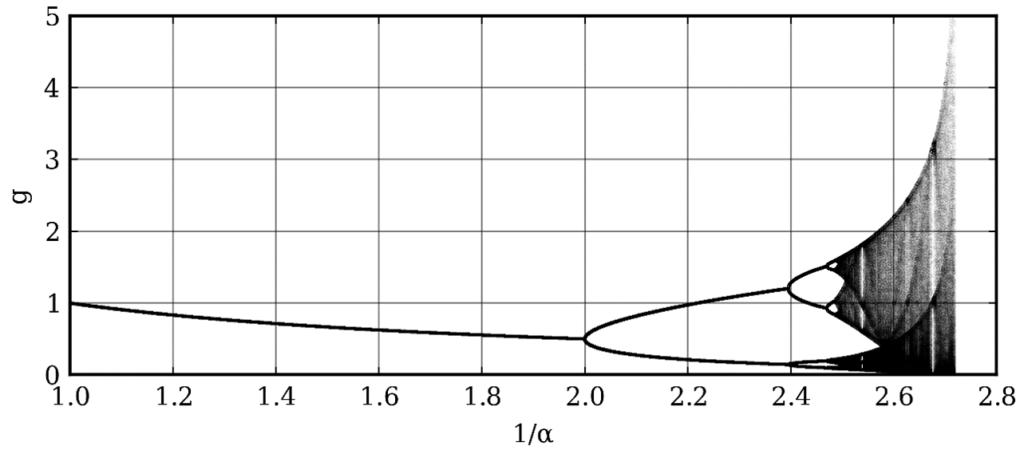


Surprisingly, it can also lead to the fact that this chaotic system orders itself. Then it can also happen that a few different phenomena occur simultaneously or repetitively one after the other. Such states are called bifurcations, which occur frequently in music, for example in multiphonics in wind instruments or in a rough voice. However, the system can also ‘agree’ on a single stable state. Then the system is called self-organized. Self-organization is also the explanation for life in general. Life sustains itself through just these mechanisms of self-organization. So for example also for NASA self-organization is the most important component of the definition of extraterrestrial life.
Musical instruments are also self-organizing systems that function by means of impulse patterns. The energy transmission of a guitar string to the soundboard is a short energy pulse, which is periodically repeated. The same is true for the piano.
In wind instruments, the mouthpiece sends a short pressure pulse into the tube, which travels down the tube, is reflected at the end, travels back to the mouthpiece, and generates a new pulse there. In musical instruments, the chaotic states are the transient processes, while the stable state is the tone. Music thus consists of a constant alternation of chaos and order.

